BOFT is a general parameter-efficient finetuning method for foundation models.
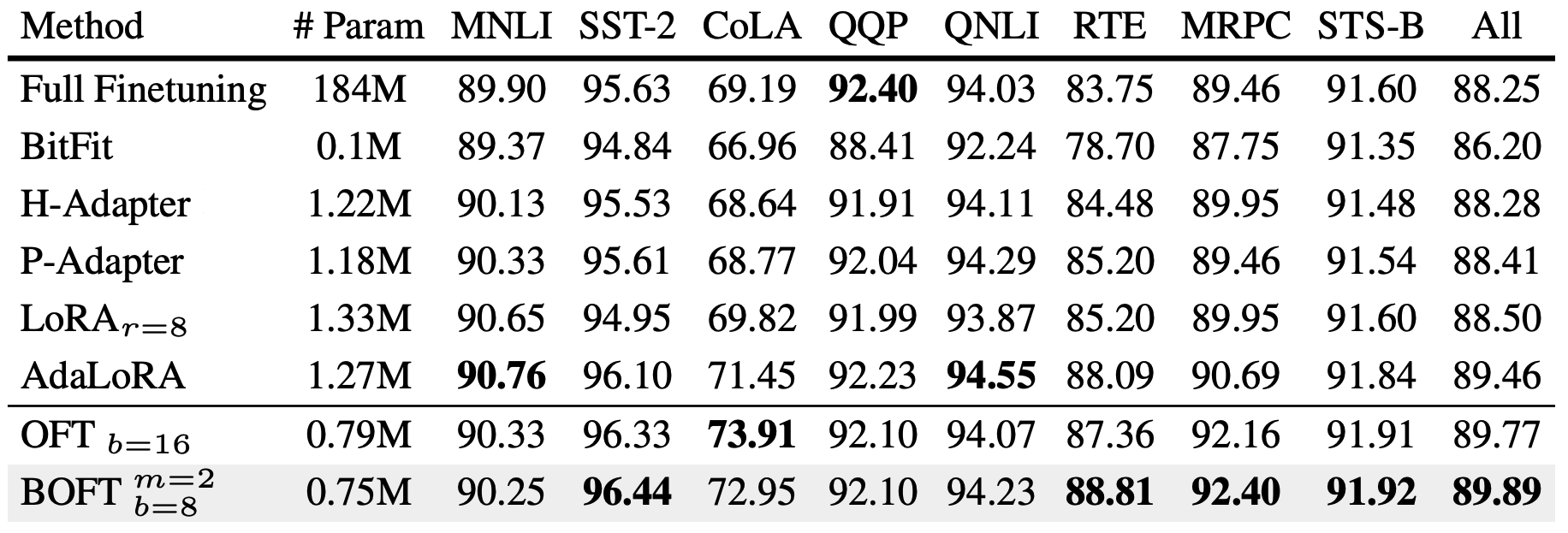
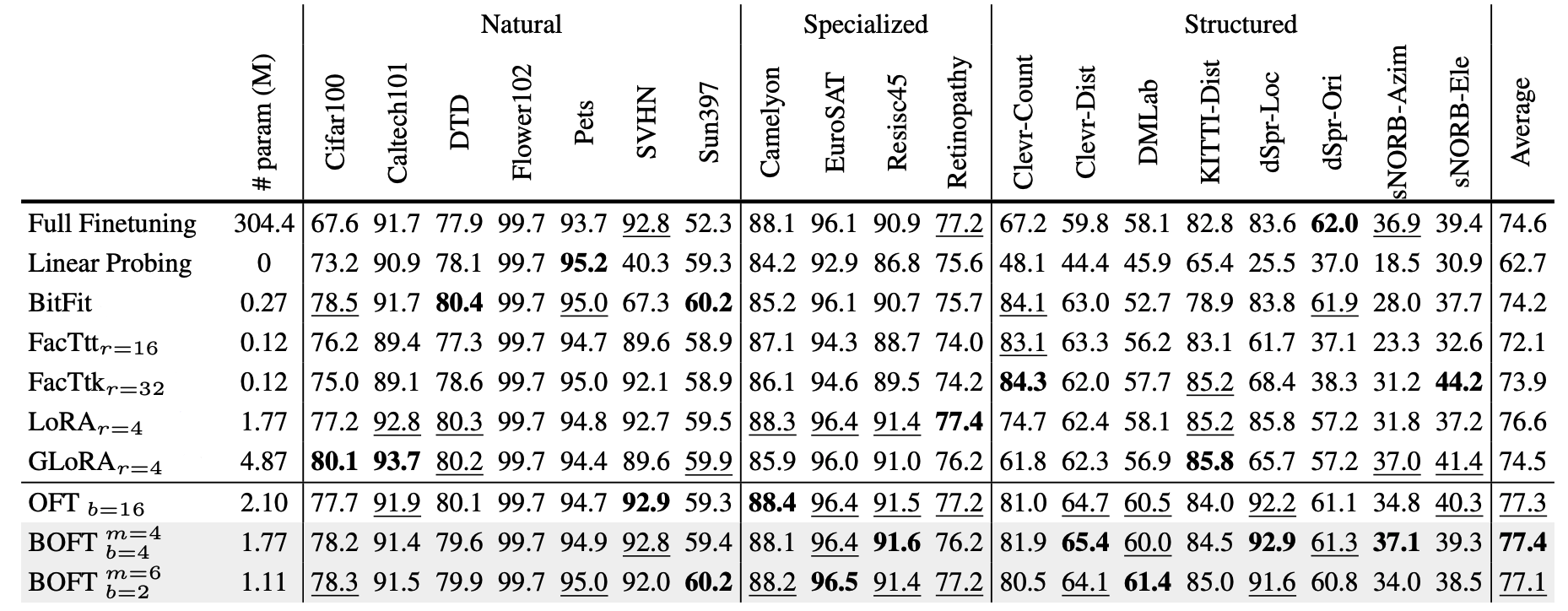
Large foundation models are becoming ubiquitous, but training them from scratch is prohibitively expensive. Thus, efficiently adapting these powerful models to downstream tasks is increasingly important. In this paper, we study a principled finetuning paradigm -- Orthogonal Finetuning (OFT) -- for downstream task adaptation. Despite demonstrating good generalizability, OFT still uses a fairly large number of trainable parameters due to the high dimensionality of orthogonal matrices. To address this, we start by examining OFT from an information transmission perspective, and then identify a few key desiderata that enable better parameter-efficiency. Inspired by how the Cooley-Tukey fast Fourier transform algorithm enables efficient information transmission, we propose an efficient orthogonal parameterization using butterfly structures. We apply this parameterization to OFT, creating a novel parameter-efficient finetuning method, called Orthogonal Butterfly (BOFT). By subsuming OFT as a special case, BOFT introduces a generalized orthogonal finetuning framework. Finally, we conduct an extensive empirical study of adapting large vision transformers, large language models, and text-to-image diffusion models to various downstream tasks in vision and language.
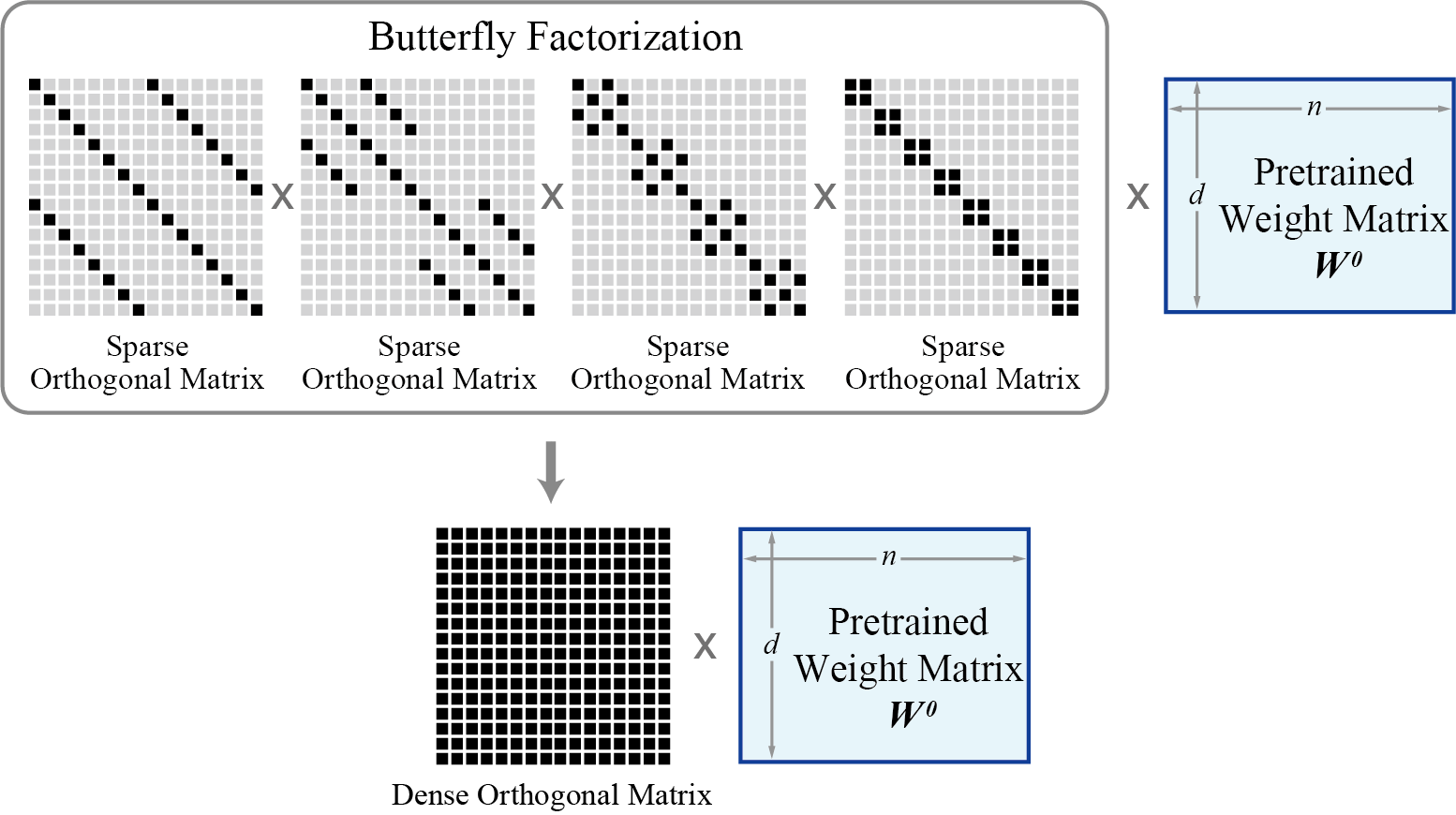
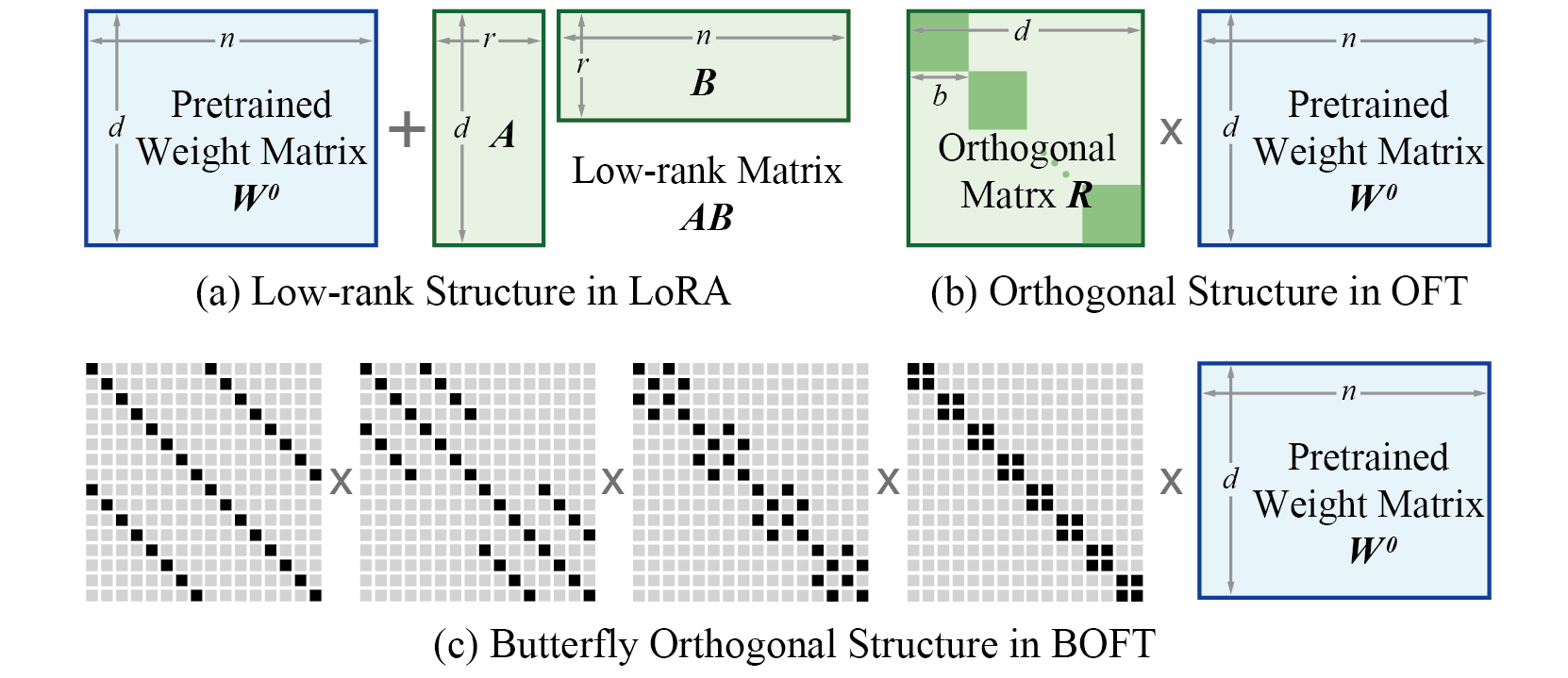
The basic idea of BOFT is to finetune the pretrained weight matrices with Butterfly-parameterized orthogonal transform. Different from previous orthogonal finetuning (OFT) that uses block-diagonal structures, BOFT uses the butterfly factorization to parameterize the orthogonal matrix, which yields a dense orthogonal matrix (in contrast, OFT has to use a sparse block-diagonal orthogonal matrix to reduce the number of trainable parameters). The butterfly parameterization of orthogonal matrices naturally generalize the original OFT framework where the block-diagonal structure now becomes a special case of BOFT. The butterfly structure serves as a smooth interpolation between different block number hyperparameters in OFT, making the orthogonal finetuning framework more flexible and more importantly, more parameter-efficient.



Model weight interpolation by setting the trained butterfly components one by one to identity matrix. We use BOFT (m=5, r=16) to finetune Stable Diffusion (SD). No retraining is performed when we gradually set each trained orthogonal matrix (B˜i) to an identity. The number in the figure denotes the number of remaining orthogonal butterfly components that has not been set to identity. Text prompt: a man with a beard smiling (for the first row) and a smiling woman (for the second row). *0 matrix is the case of SD with a learned control head.


@InProceedings{liu2024boft,
author = {Liu, Weiyang and Qiu, Zeju and Feng, Yao and Xiu, Yuliang and Xue, Yuxuan and Yu, Longhui and Feng, Haiwen and Liu, Zhen
and Heo, Juyeon and Peng, Songyou and Wen, Yandong and Black, Michael J. and Weller, Adrian and Sch{\"o}lkopf, Bernhard},
title = {Parameter-Efficient Orthogonal Finetuning via Butterfly Factorization},
booktitle = {ICLR},
year = {2024}
}